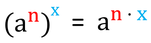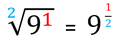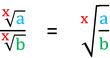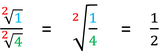Potenz- und Wurzelgesetze
➥ Merk dir:
Potenzgesetze kompakt
Potenzen mit gleicher Basis werden multipliziert, indem man die Exponenten addiert. Die Basis bleibt gleich.
Potenzen mit unterschiedlicher Basis und gleichem Exponenten werden multipliziert, indem man die Basis multipliziert. Der Exponent bleibt gleich.
Potenzen mit gleicher Basis werden dividiert, indem man die Exponenten subtrahiert, die Basis bleibt gleich.
Potenzen mit unterschiedlicher Basis und gleichem Exponenten werden dividiert, indem man die Basis dividiert, der Exponent bleibt gleich.
Potenzen werden potenziert, indem man die Exponenten multipliziert.
Besondere Potenzen sind:
x0 = 1 mit x ≠ 0
x1 = x
Zehnerpotenzen sind Potenzen mit der Basis 10.
Sie werden genutzt, um sehr kleine oder sehr große Zahlen übersichtlich darzustellen.
Potenzen
Potenzen sind die sogenannten "Hochzahlen", ein Ausdruck, der in der Schule manchmal in den kleineren Klassen verwendet wird.
Fachlich korrekt heißen sie Potenzen und sie werden so geschrieben:
xn
x ist die Basis und n der Exponent.
Und so und nicht anders werden sie auch hier bezeichnet. Merk sie dir also gleich, damit du mir im weitern Verlauf folgen kannst.
Potenzen sind eine Zusammenfassung der Multiplikation gleicher Zahlen bzw. Variablen:
7 ⋅ 7 ⋅ 7 ⋅ 7 ⋅ 7 = 75 oder x ⋅ x ⋅ x ⋅ x = x4
Das geht auch umgekehrt, z.B.:
123 = 12 ⋅ 12 ⋅ 12 oder x8 = x ⋅ x ⋅ x ⋅ x ⋅ x ⋅ x ⋅ x ⋅ x
Sehr wichtig ist hier die Unterscheidung zwischen der Zusammenfassung der Addition und der Zusammenfassung der Multiplikation:
Addition zusammenfassen: x + x + x = 3x
Multiplikation zusammenfassen: x ⋅ x ⋅ x = x3
Es macht also einen gewaltigen Unterschied, wohin man die 3 schreibt!
Merk dir das auf jeden Fall!!!
Besondere Potenzen, die man kennen muss
Es sind vor allem 2, die man kennen muss:
x0 = 1 (x ≠ 0)
Erklärung: Hoch Null ergibt immer 1, egal, welche Zahl die Basis bildet!
Einzige Ausnahme: Die Basis selbst darf nicht Null sein, das ist verboten!
Beispiele:
60 = 1
(-4)0 = 1
(¾)0 = 1
7.562.1280 = 1
x1 = x
Erklärung: Hoch 1 kann man hinschreiben oder weglassen, es ist dasselbe!
Beispiele:
61 = 6
(-4)1 = -4
(¾)1 = ¾
7.562.1281 = 7.562.128
Potenzgesetze
Die Potenzgesetze umfassen sowohl die Gesetze, die man für Potenzen anwenden muss, als auch die Gesetze, die man für die Berechnung von Wurzeln anwenden muss. Wurzeln sind die Gegenoperation zu den Potenzen, so wie die Addition und Subtraktion Gegenoperationen sind oder die Multiplikation und Division.
Das werden jetzt eine Menge Buchstaben, lass dich davon nicht verwirren, ich erkläre dir jedes Gesetz weiter unten Schritt für Schritt.
Addition und Subtraktion von Potenzen
Potenzen werden NUR DANN addiert oder subtrahiert, wenn Basis UND Exponent gleich sind!!! Weder an der Basis noch am Exponenten ändert sich hierbei etwas, sie werden nur zusammengezählt. So, wie man auch andere Variablen zusammenzählt:
x2 + x2 = 2x2
7x4 - 2x4 = 5x4
So etwas geht nicht:
x3 + x4 = keine Lösung, bleibt so!
Multiplikation von Potenzen
1. Potenzgesetz: Multiplikation von Potenzen mit gleicher Basis
ax · ay = ax+y
Was bedeutet das?
Wenn man zwei Potenzen mit gleicher Basis (a) multipliziert,
dann werden die Exponenten (x und y) addiert.
Beispiele zum ersten Potenzgesetz:
54 · 53 = 54+3= 57
x2 · x6 = x2+6 = x8
46 · 45 · 43 = 46+5+3 = 414
y0,5 · y1,5 · y6 = y0,5+1,5+6 = y8
2. Potenzgesetz: Multiplikation von Potenzen mit gleichem Exponenten
ax · bx = (a · b)x
Was bedeutet das?
Wenn man zwei Potenzen mit unterschiedlicher Basis (a), aber gleichem Exponenten multipliziert, dann werden die Basiszahlen multipliziert, der Exponent aber bleibt unverändert.
Warum muss man eine Klammer setzen?
Weil sich der Exponent auf beide Zahlen bezieht! Ohne Klammer würde man nur die 2. Zahl potenzieren.
Beispiele zum zweiten Potenzgesetz:
54 · 64 = (5 · 6)4 = 304
x4 · y4 = (x · y)4 = xy4
Man kann beide Gesetze in einer Aufgabe zusammen haben. Beispiel:
x4 · x2 · y6 = x6· y6 = (x · y)6 = xy6
Erklärung: Die beiden ersten Variablen der Aufgabe haben die gleiche Basis (x), hier wendet man das 1. Potenzgesetz an. Dann haben wir unterschiedliche Basis (x und y), aber gleichen Exponenten (6). Hier kommt das 2. Potenzgesetz zur Anwendung.
Division von Potenzen
3. Potenzgesetz: Division von Potenzen mit gleicher Basis
ax : ay = ax-y
Was bedeutet das?
Wenn man zwei Potenzen mit gleicher Basis (a) dividiert,
dann werden die Exponenten (x und y) subtrahiert.
Beispiele zum dritten Potenzgesetz:
54 : 53 = 54-3= 51 = 5
x2 : x6 = x2-6 = x-4
46 : 45 · 43 = 46-5+3 = 44
y8,5 · y1,5 : y6 = y8,5+1,5-6 = y4
4. Potenzgesetz: Division von Potenzen mit gleichem Exponenten
ax : bx = (a : b)x
Was bedeutet das?
Wenn man zwei Potenzen mit unterschiedlicher Basis (a), aber gleichem Exponenten dividiert, dann werden die Basiszahlen dividiert, der Exponent aber bleibt unverändert.
Warum muss man eine Klammer setzen?
Weil sich der Exponent auf beide Zahlen bezieht! Ohne Klammer würde man nur die 2. Zahl potenzieren.
Beispiele zum vierten Potenzgesetz:
124 : 64 = (12 : 6)4 = 24
x4 : y4 = (x : y)4 = (x/y)4
Man kann beide Gesetze in einer Aufgabe zusammen haben. Beispiel:
x8 : x2 : y6 = x6 : y6 = (x : y)6 = = (x/y)6
Erklärung: Die beiden ersten Variablen der Aufgabe haben die gleiche Basis (x), hier wendet man das 3. Potenzgesetz an. Dann haben wir unterschiedliche Basis (x und y), aber gleichen Exponenten (6). Hier kommt das 4. Potenzgesetz zur Anwendung.
Potenzieren von Potenzen
Was bedeutet das?
Potenzen werden potenziert, indem man die Exponenten multipliziert:
Beispiele zur Potenzierung von Potenzen:


Potenzieren von Klammern
Negative Exponenten
Zehnerpotenzen
Zehnerpotenzen sind alle Potenzen mit der Basis 10. Die sind sehr wichtig, um sehr große oder sehr kleine Zahlen darstellen zu können.
Sehr große Zahlen werden mit positiven Exponenten dargestellt.
Sehr kleine Zahlen werden mit negativen Exponenten dargestellt.
Man kann aber stattdessen auch bestimmte Wörter nutzen. Das soll hier mal kurz zusammengefasst werden, von groß zu klein:
Peta = 1 Billiarde = 1.000.000.000.000.000 = 1015 (eine 1 mit 15 Nullen)
Tera = 1 Billion = 1.000.000.000.000 = 1012 (eine 1 mit 12 Nullen)
Giga = 1 Milliarde = 1.000.000.000 = 109 (eine 1 mit 9 Nullen)
Mega = 1 Million = 1.000.000 = 106 (eine 1 mit 6 Nullen)
Kilo= 1 Tausend= 1.000 = 103 (eine 1 mit 3 Nullen)
1 Hundert = 100 = 102 (eine 1 mit 2 Nullen)
Zehn = 10 = 101 (eine 1 mit 1 Null) oder auch nur 10
Eins = 1 = 100 (eine 1 mit 0 Nullen) oder auch nur 1
dezi = 0,1 = 10-1 (eine 1 als erste Stelle nach dem Komma)
centi = 0,01 = 10-2 (eine 1 als zweite Stelle nach dem Komma)
milli = 0,001 = 10-3 (eine 1 als dritte Stelle nach dem Komma)
mikro = 0,000001 = 10-6 (eine 1 als sechste Stelle nach dem Komma)
nano = 0,000000001 = 10-9 (eine 1 als neunte Stelle nach dem Komma)
piko = 0,000000001 = 10-12 (eine 1 als zwölfte Stelle nach dem Komma)
femto = 0,000000000001 = 10-15 (eine 1 als fünfzehnte Stelle nach dem Komma)
Wie rechnet man mit Zehnerpotenzen?
Supereasy!
Der Exponent zeigt dir immer, wie viele Stellen nach rechts (positive Exponenten) oder nach links (negative Exponenten) man ein Komma verschieben und eventuell mit Nullen auffüllen muss. Ich zeige dir Beispiele:
3 · 100 = 3
Überlegung: Die 10 hat eine 0 als Exponenten, also wird das Komma nicht verschoben - die 3 bleibt.
3 · 101 = 30
Überlegung: Die 10 hat eine 1 als Exponenten, also wird das Komma um 1 Stelle nach rechts verschoben und eine 0 angefügt.
3 · 102 = 300
Überlegung: Die 10 hat eine 2 als Exponenten, also wird das Komma um 2 Stellen nach rechts verschoben und zwei Nullen angefügt.
3 · 10-2 = 0,03
Überlegung: Die 10 hat eine -2 als Exponenten, also wird das Komma um 2 Stellen nach links verschoben und die entstehende Lücke mit 0 gefüllt.
3 · 10-4 = 0,0003
Überlegung: Die 10 hat eine -4 als Exponenten, also wird das Komma um 4 Stellen nach links verschoben und die entstehenden Lücken mit Nullen gefüllt.
Soweit zu den ganzen Zahlen.
Was aber macht man mit Dezimalzahlen?
Man geht genau gleich vor:
12,57 · 101 = 125,7
Überlegung: Die 10 hat eine 1 als Exponenten, also wird das Komma um 1 Stelle nach rechts verschoben.
12,57 · 102 = 1.257
Überlegung: Die 10 hat eine 2 als Exponenten, also wird das Komma um 2 Stellen nach rechts verschoben.
12,57 · 10-1 = 1,257
Überlegung: Die 10 hat eine -1 als Exponenten, also wird das Komma um 1 Stelle nach links verschoben.
12,57 · 10-2 = 0,1257
Überlegung: Die 10 hat eine -2 als Exponenten, also wird das Komma um 2 Stellen nach links verschoben.
Ok, und wie geht man bei Brüchen vor?
Am einfachsten ist: Man lässt sie so stehen. Das ist genau. Oder man rechnet den Bruch in eine Dezimalzahl um und geht dann vor wie bei den Dezimalzahlen.
Was mache ich mit den Wörtern Mega, milli usw.?
Das habe ich oben beschrieben, aber hier will ich dir zeigen, wie man die anwendet. Man kann diese Begriffe direkt durch die Zahl ersetzen. Man kann sich z.B. überlegen, dass Kilometer aus 2 Wörtern besteht: Kilo und Meter. Kilo ist dasselbe wie 1.000, also weiß man: 1 Kilometer = 1.000 Meter.
Umgekehrt geht es genauso: 1 Millimeter = 0,001 Meter.
Man ersetzt also das Wort durch die entsprechende Zahl. Das gilt bei allen Wörtern, denen solche Begriffe voranstehen!
3 kg = 3.000 g
7 femtometer (7 fm) = 0,000000000007 m (besser überschaubar: 7 · 10-15 m)
Wurzelgesetze
Die Wurzel (√) in der Mathematik ist ein besonderes Zeichen mit einigen Begriffen, die man kennen muss:
Es gibt beim Wurzelziehen eine wichtige Bedingung: Der Radikand x darf niemals negativ sein, er muss also undbedingt gleich oder größer als 0 sein.
Mathematisch wird diese Bedingung so dargestellt:
x ≥ 0
Die häufigste Wurzel ist die 2. Wurzel, die man Quadratwurzel nennt.
Sie kann auf 2 Arten geschrieben werden:

Meist wird die Variante ohne die kleine 2 oben rechts gewählt.
Die dritte Wurzel heißt Kubikwurzel, ab der 3 muss der Wurzelexponent immer dazugeschrieben werden.
Doch was genau ist nun das Wurzelziehen?
Die Wurzel ist die Gegenoperation zum Potenzieren.
Das heißt, dass beim Ziehen der Wurzel aus einer Potenz wieder die ursprüngliche Zahl herauskommt:
32 = 9
Wenn man aus dem Ergebnis 9 die Wurzel zieht, kommt wieder 3 heraus:
√9 = 3
Statt des Wurzelzeichens √ kann man auch eine Potenz schreiben:

Die Potenz ist für das Wurzelziehen stets ein Bruch. Die beiden zahlen des Bruchs (Zähler und Nenner) haben dabei unterschiedliche Bedeutungen:
Zähler = Exponent
Nenner = Wurzelexponent
Das heißt für die beispielhafte Potenz 9½, wenn man das korrekt ausschreibt:
Hier sind noch andere Beispiele:

Ausgesprochen ist das wie folgt:
Fünf hoch drei Viertel = vierte Wurzel aus fünf hoch drei.
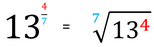
Ausgesprochen ist das wie folgt:
Dreizehn hoch vier Siebentel = siebente Wurzel aus dreizehn hoch vier.

Ausgesprochen ist das wie folgt:
Einhundertfünfundzwanzig hoch zwei Neuntel = neunte Wurzel aus einhunderfünfundzwanzig zum Quadrat.
Damit gelten auch für die Wurzeln die Potenzgesetze: Man kann jede Wurzel umschreiben in eine Potenz und dann die Gesetze anwenden.
Oder man wendet die Wurzelgesetze an, wenn man nicht umschreiben möchte. Die zeige ich dir jetzt.
Addition und Subtraktion von Wurzeln
Wurzeln dürfen nur addiert und subtrahiert werden, wenn Radikand UND Wurzelexponent gleich sind.
Sie werden wie gleiche Variablen zusammengezählt bzw. voneinander abgezogen.